Вестник № 7 / 2000
БИБЛИОТЕКА РО
Формирование понятия числа на основе изучения отношения величин
Минская
Г.И.
Понятие о целом положительном числе является основополагающим для всего курса арифметики в начальных классах. Опираясь на это понятие и некоторые свойства десятичной системы счисления, дети в течение четырех лет осваивают приемы вычислений, умения складывать и вычитать, умножать и делить числа. Способы введения понятия о числе и счете в I классе разработаны в методике преподавания арифметики особенно детально. Имеется большая психологическая литература относительно условий формирования начального понятия о числе и первых навыков счета. Казалось бы, этот раздел программы и методики преподавания арифметики является прочно обоснованным и установившимся. И действительно, на протяжении нескольких десятилетий он оставался по существу без изменений, таким, каким представлен, например, в учебнике А.С. Пчелко и Г.Б. Поляка для I класса [6] и в соответствующей методике А.С. Пчелко [7]. Методические изыскания шли в основном по линии улучшения тех или иных частных приемов изложения установленного программного содержания.
Однако психологические исследования, проведенные в последнее время как у нас, так и за рубежом, выявили ряд обстоятельств, позволяющих, с одной стороны, критически рассмотреть принятое содержание первых разделов курса арифметики, с другой – наметить новые пути введения понятия о числе в этот курс. В некоторых исследованиях (например, в работах П.Я. Гальперина и Л.С. Георгиева [1], В.В. Давыдова [2]) специально изучалось то, на какой признак сосчитываемого ряда объектов ориентируются дети, освоившие счет и числа по принятой программе и методике (в детском саду и в школе). Было обнаружено, что таким признаком для многих детей является пространственно-временная замкнутость, отделенность какой-либо вещи от всех других, входящих в наличную совокупность. Эти дети, хорошо владеющие пересчитыванием отдельных предметов и имеющие отчетливые “представления” о каждом числе (например, в пределе 10—15), либо не умели произвести счет совсем, либо делали грубые ошибки, если в предъявленной им задаче требовалось пересчитать предметы по основанию, отличающемуся от отдельного элемента совокупности.
Психологический анализ причин, приводящих к “срыву” ранее сформированного действия, показал, что в их основе лежит своеобразное явление – отождествление ребенком множества единиц, как элементов ряда числительных, с частями самой реальной совокупности. Эти дети не различают объект счета и средство особого изображения его результата, т.е. стандартное (типовое) множество отдельных единиц. Единица отождествляется ими с отдельными элементами пересчитываемой группы. Поэтому, например, группа кубиков, заданная как объект счета вопросом “сколько?”, определяется только числом “б”, ибо в уме дети “уточняли” вопрос на основании наглядно-данного отдельного кубика и находили, что таких “единиц” здесь “б”.
Легко видеть, что такое “уточнение” и ответ возможен лишь тогда, когда ребенок заранее отождествляет единицу (числительное “один”) с отдельным элементом самой группы (кубик). Числительное выступает здесь лишь как новое название этого отдельного предмета.
Вместе с тем группа кубиков сама по себе может быть определена в принципе любым числом в зависимости от того, что будет принято за основание счета, какая будет выбрана мера. Последняя же может и не совпадать с “отдельным” кубиком. Так, если основанием выбрать “прямоугольник” (рис. 1), то группа кубиков определяется числом “I”. В других случаях она может определяться числом “2” (сколько горизонтальных рядов) и числом “З” (сколько вертикальных рядов).
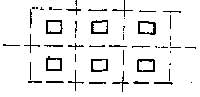
Рис. 1. Возможность описания одной и той же группы предметов разными числами (в зависимости от основания счета).
Здесь наличная группа определяется некоторой совокупностью единиц (1, 2, 3, 6), но теперь последние фиксируют отношение объекта счета к любому наперед установленному основанию (мере). Эти единицы – как отдельности – особым образом моделируют указанное отношение и не сливаются с реальными, физически отдельными предметами, составляющими объект счета. Именно поэтому, в частности, любая группа элементов может быть обозначена отдельной единицей (как “один”), если основанием счета также выбрана “дробная” мера.
Механизм счета как умственного действия таков (см. [3]), что при его полноценном формировании человек уже без специальных и развернутых указаний самостоятельно выделяет любое нужное основание счета (“нужное” – по условиям практической задачи) и работает с этим основанием, находя без особых сознательных усилий отношение объекта к этому основанию. Возможность быстрой и свободной смены оснований счета, учет зависимостей, существующих между объектом, мерой и числом, показывают, что человек владеет самой формой числа как особым средством моделирования отношений конкретных физических объектов.
К сожалению, как отмечалось выше, многие первоклассники не владеют этой формой. В этом, на наш взгляд, во многом повинна принятая программа и методика обучения арифметике, не учитывающая действительного психологического механизма счета как умственного действия и условий его полноценного формирования. Эта методика такова, что в процессе обучения у детей не формируется различение объекта счета, основания счета и средств, изображающих их отношение. Поэтому их счет оказывается неполноценным, ибо не содержит точных ориентиров для гибкой смены оснований, для понимания зависимости получаемой числовой характеристики объекта от смены основания счета.
Как известно, согласно обычной методике, овладение счетом (до 10) включает:
1) знание названий первых десяти чисел и их последовательности;
2) понимание, что при пересчитывании совокупности последнее произнесенное слово (числительное) означает, сколько всего предметов в данной совокупности;
3) знание места каждого числа в натуральном ряде;
4) наличие представления о величине совокупности, обозначением которой это число является [7, стр. 143].
Рассмотрим наиболее характерные пункты этого перечня. Пункт 2 требует, чтобы ребенок понимал полученное числительное как обозначение количества предметов в данной совокупности, т. е. количества ее отдельных элементов. Это обстоятельство подчеркивается и в пункте 4: ребенок должен иметь представление о величине совокупности, обозначаемой данным (именно данным) числом. Следовательно, зная число “5”, ребенок обязан представлять соответствующую ему “величину” совокупности. Здесь акцент опять ставится на то, что числовая характеристика есть непосредственная характеристика совокупности, ее прямое, наглядное свойство.
Впрочем, это методическое требование наиболее реально обнаруживается в следующем факте. Изучая числа в пределе 100, дети связывают воедино 100 конкретных спичек – их связка, очевидно, должна дать ребенку “наглядное” представление о величине числа “100” (см. стр. 133 [6]).
Абстракция числа понимается здесь как прямое отвлечение некоторого непосредственного свойства совокупности, так сказать “объема”, количества составляющих ее отдельных элементов. Ясно, что средством такого отвлечения, согласно требованиям классической сенсуалистической теории абстракции, должно быть сопоставление многих совокупностей по “объему” входящих в них элементов, т. е. выделение общего, одинакового момента, чем и является “абстрактное” представление о числе отдельных элементов. В учебнике с первых страниц дается именно эта схема выделения числовой характеристики совокупностей. Так, группа мальчиков сопоставляется с группой колес велосипеда, с группой палочек и группой точек. Что может быть общего, одинакового у этих столь разнокачественных совокупностей? Ничего, кроме количества отдельных составляющих их абстрактных элементов. Оно равно “2”. Это число характеризует такое непосредственное свойство любой из этих совокупностей, как их “величину”.
Аналогичным образом дети знакомятся со всеми числами до 10. Во всех этих случаях число выступает как абстрактное определение “величины” совокупности, выступающей при сопоставлении ее отдельных элементов – единиц с единицами других совокупностей 1.
Эта программа и методика, реализуемые в практике обучения, как раз и приводят к тому, что многие дети-первоклассники при наличии “хорошего” счета (по обычному стандарту) вместе с тем отождествляют число (множество единиц) с реальной совокупностью, не различают объекта счета и средств фиксации его результата, не умеют выделять любые основания счета и свободно переходить от одного основания к другому, не понимают зависимости числа от выбранного основания. В результате эти дети не получают полноценного понятия о числе, что отрицательно сказывается затем на всем последующем усвоении арифметики. В частности, эти дети, как показывают наблюдения, с трудом осваивают операции с именованными числами, с трудом понимают связь целых и дробных чисел.
Традиционный способ знакомства детей с числом имеет и более серьезные отрицательные последствия. В частности, мы полагаем, что к ним в полной мере относятся те дефекты традиционного введения чисел, которые отмечает А.Н. Колмогоров (непосредственно он говорит о недостатках введения понятия о действительном числе, но, с нашей точки зрения, они имеют глубокие корни еще при знакомстве ребенка с целым положительным числом): “Что общепринятая система [введения числа. – Г.М.] с педагогической стороны дефектна, видно хотя бы из тех трудностей, которые затем возникают при усвоении учащимися независимости смысла геометрических и физических формул от выбора единиц измерения и понятия “размерности” геометрических и физических формул” (из предисловия А. Н. Колмогорова к книге А. Лебега “Об измерении величин”, изд. 2. – М.: Учпедгиз, 1960. – С. 10).
Естественно, встает задача: нельзя ли – пока в экспериментальном порядке – сформировать у первоклассников адекватную ориентировочную основу счета, т. е. сформировать такое понятие о числе, которое послужило бы полноценной основой счета как умственного действия 2. Определенную попытку в этом направлении представляла та работа, которую под нашим руководством провела учительница А.П. Путилина в I классе школы № 11 г. Тулы (1962/63 уч. год). Преподавание математики в этом классе осуществлялось по особой экспериментальной программе. Все первое полугодие I класса и еще до введения числа дети знакомились с основными величинами (длиной, объемом, весом и т. д.), со способами их сравнения и изображения результата сравнения буквенными формулами равенства-неравенства. Дети знакомились с основными свойствами равенства-неравенства, с возможностью и условиями перехода от равенства к неравенству и от неравенства к равенству 3. И лишь во втором полугодии они знакомились с числом.
В данном разделе излагаются особенности введения числа по экспериментальной программе и результаты опытного обучения3.
Еще до начала учебных занятий в I классе (а затем в ходе занятии, но без специального обучения) мы проверили знания учащихся в области счета. Оказалось, что многие дети практически были знакомы с рядом числительных от 1 до 10, умели произносить их в прямом, а некоторые дети и в обратном порядке. У многих детей имелось представление о возможности применения числительных к сосчитыванию предметов, что они и делали при прямом задании: сосчитать небольшую группу предметов (до 4 – 7). Вместе с тем многие дети плохо ориентировались в соотношениях чисел: “Что меньше – 5 или 9?”, особенно за пределами первого десятка (16 или 18? 19 или 15?). Отметим, что к началу работы над разделами экспериментальной программы, связанными с формированием счета, все учащиеся “стихийно” научились называть числительные от 1 до 12—15 и далее.
Общий раздел программы, связанный с числом, был разбит нами на ряд тем. Отметим, что поскольку в основе нашего способа введения числа лежало обучение детей поиску отношения того или иного объекта (величины) как целого к его части (мерке), то в определенном смысле число и счет вводились на основе измерения величин. Но фактически это не было измерением в точном смысле слова, ибо последнее предполагает фиксированную единицу измерения (чего у нас вначале не было) и, как правило, соотносимо только с непрерывными объектами (мы же обучали детей искать указанное отношение и при дискретных объектах). В нашу задачу не входит анализ связи счета и измерения. Отметим лишь, что во всем последующем изложении (как и в самом обучении) мы употребляем термины “измеряемый объект”, “мерка” как очень удобные для обозначения содержания тех предметов и действий с ними, которые вводились экспериментальной программой.
Приступая к описанию хода обучения и указанию его основных этапов, мы не анализируем всех его оснований. Подробно структура счета и связь с ним числа рассмотрена в работе В.В. Давыдова [2], к которой мы и отсылаем читателя. Наша экспериментальная программа являлась практическим следствием этого теоретического анализа.
С конца января второго полугодия 1962/63 учебного года учащиеся экспериментального класса приступили к изучению следующих тем:
1. Задачи, требующие определения отношения величины (измеряемого объекта) и мерки. Обучение особой операции по выявлению этого отношения (работа с меркой, правила фиксации результата и т. д.). Изображение отношения стандартным множеством предметных единиц.
2. Использование слов-числительных для обозначения результата счета.
Первая тема несколько необычна. Ее смысл состоит в том, чтобы мотивировать ребенку необходимость перехода к числительным как особым “орудиям” математики. Так, на первом уроке этой темы перед всеми детьми ставилась задача – выбрать из деревянных планок, находящихся в коридоре, такую, которая по длине была бы равна такому-то образцу Условие задачи – образец с собой брать нельзя! Как быть?
Другая задача: налить в банку столько воды, сколько уже есть в другой банке (банки различны по форме и диаметру, по “высоте” столбика воды здесь судить о равенстве объемов нельзя). Как это сделать?
В серии аналогичных ситуаций дети подводились к мысли о том, что уравнивание можно производить не только непосредственно (путем накладывания образца на материал при сопоставлении по одному из признаков), но и косвенным, опосредствованным путем. С помощью наводящих вопросов учитель наталкивал учащихся на выявление основного условия реализации такого пути – на выбор особой мерки, работая с которой можно осуществлять опосредствованное уравнивание.
Дети учились отмечать каждое накладывание мерки маленьким кубиком. В результате образовались кучки кубиков, и дети узнавали, что с их помощью теперь уже можно отобрать в коридоре “такую же” палочку или налить “столько же” воды. Они быстро осваивали технику отмеривания, опираясь на результат предыдущего измерения (на совокупность кубиков).
Для усвоения этой темы потребовалось всего два урока. Правда, учитель не ставил себе задачи на этих уроках привить детям все правила работы с меркой – усвоение всех “тонкостей” техники относилось к следующим урокам. Но уже здесь ребята усвоили, что кубик выкладывается только тогда, когда мерка целиком укладывается на образце (или материале) или полностью заполняется водой (в случае работы с водой). В противном случае остаток не учитывается.
Учитель постоянно подчеркивал необходимость фиксации результата измерения (поиска отношения) кубиками. Все дети хорошо понимали их назначение. При этом некоторые из них выкладывали не кубики, а другие предметы – учитель специально обращал внимание детей на допустимость “подмены”. В этом случае любые отдельные предметы могли изображать результат измерения.
Вместе с тем в ряде заданий учитель показывал, что и мерку можно брать любую (в пределах практического удобства). Однако, выбрав определенную мерку, последующую работу (измерение и отмеривание) можно выполнять только с нею. Основная цель работы по этой теме состояла в том, чтобы дети с самого начала научились четко различать измеряемый объект, мерку и средство фиксации их отношения. Предметное множество единиц так сказать “телесно” воплощает в себе наличие таких средств, и в самом начале это обстоятельство специально выделялось учителем. Он задавал вопрос: “Сколько таких мерок (показывает) уместилось здесь (в измеряемом предмете)?” Дети показывают кучку кубиков или группу других предметов: “Вот столько!”
В этот период учитель предлагал детям “измерять” дискретные объекты (группу кубиков, квадратов), причем мерка могла быть составной (например, состоять из двух кубиков). В этом случае “накладывание” составной мерки на объект все равно требовало отметки отдельным кубиком. Совокупность отдельных кубиков (единиц) выражала отношение группы предметов к составной мерке. Опираясь на эту совокупность и мерку, дети могли получать новую группу, равную первой (рис. 2). Здесь особенно отчетливо выступало различие между тем, что и чем “измеряется”, и отдельными единицами, изображающими результат действия.
Следующая тема включала замену предметных единиц словами-числительными и более тщательную отработку поиска соотношения мерки и части измеряемого объекта, приводящего к понятию “один”.
Введение числительных мотивировалось тем, что “единицы-кубики” не совсем удобны (рассыпаются; иногда их нужно много; их невозможно вложить в письмо, если требуется сообщить о результате измерения, и т.п.). Учитель показал детям, что все правила работы с мерками остаются теми же, только вместо кубиков произносятся слова: “раз”, “раз”. Но в этом случае мы не знаем, сколько “раз” уложилась мерка: ведь эти “раз” можно произносить без конца (здесь обнаруживается отличие временной развертки единиц – ибо слово здесь есть единица – от пространственной). Нужно отличать эти “раз” – один раз, два раза, три раза и т.д.
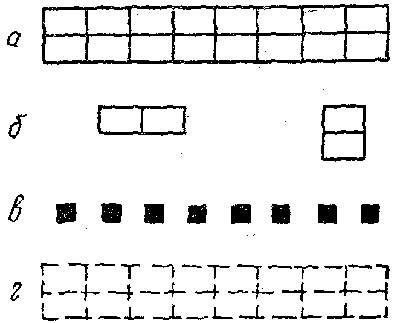
Рис 2. Использование стандартной совокупности предметных единиц:
а) исходный
объект – образец;
б) основания счёта;
в) результат счёта – стандартная совокупность;
г) объект, воспроизведённый по образцу.
А можно говорить без “раз” – просто один, два, три..., имея в виду, что мы каждым словом отмечаем накладывание мерки на предмет. Последнее слово (например, семь) говорит о том, сколько мерок содержится в предмете. Для решения задачи на уравнивание эту мерку нужно вновь брать семь раз – отмеривать до тех пор, пока в указанном порядке не дойдем до слова семь.
Выполняя ряд упражнений, ученики быстро освоились с правилами употребления числительных (их названия и последовательность были известны детям до этого). В некоторых случаях учитель просил заменять слова кубиками или палочками, и дети вновь переходили к предметному множеству единиц. Правда, теперь они уже пересчитывали эти кубики и палочки (например, говорили “пять”). Тогда учитель задавал новый вопрос: “А как ты получил эти кубики, почему же их оказалось пять, о чем говорят эти кубики?” После этого следовали точные ответы.
Особое внимание обращалось на тщательное соблюдение правил работы с составными мерками и на дискретных объектах. Так, на одном уроке в качестве измеряемого предмета по длине были выбраны 16 кубиков, положенных в ряд. Меркой служил ряд из трех кубиков. Дети, работая этой меркой, установили, что получится число 5 и еще остаток. Они сами сделали вывод, что отдельный кубик считать нельзя: “Нельзя сказать, что это шесть – ведь это не по мерке”.
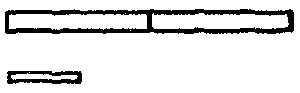
Рис. 3
Приведем
выдержку из протокольной записи урока от 30/1 1963 года.
Учитель. Возьмите две палочки (по 10 см) и вот так положите их
на парте вместе— сложите по длине (показывает на доске, рис. 3). Это будет
ваш измеряемый предмет. Мерка такая (5 см), покажите ее (проверяет,
все ли взяли нужную мерку). Сосчитайте про себя, сколько таких мерок содержится
в измеряемом предмете.
Саша С. Четыре раза уложилась наша мерка!
Учитель. Так, а теперь покажите два из четырех – по нашей мерке.
Саша В., Лена П., Надя М. поднимают обе планки – весь измеряемый предмет; остальные ученики выполняют задание правильно.
Учитель. Лена, покажи ребятам два по нашей мерке.
Лена П. быстро убирает одну планку.
Учитель. Ты покажи, как сначала сделала. Правильно так, дети?
Ученики. Нет!
Учитель. Почему же неверно?
Наташа П. Потому что это четыре!
Учитель По какой мерке?
Наташа П. По этой (показывает планку в 5 см.).
Учитель. Покажите “один” по нашей мерке!
Ученики зажали нижнюю часть планки в кулак – закрыли ее пальцами другой руки, показали половину планки.
Учитель. Теперь измеряемый предмет тот же, а мерка такая (10 см). Сколько раз она поместилась в этом же измеряемом предмете?
Саша Б. У меня мерка два раза поместилась!
Учитель. А у тебя, Оля?
Оля Н. Два раза!
Учитель. Как же понять – было четыре, а теперь два?
Лена П. Разные мерки!
Учитель. В первый раз какая была мерка?
Ученики. Маленькая!
Учитель. А сколько раз она поместилась?
Ученики. Четыре!
Учитель. А во второй раз?
Ученики. Большая!
Учитель. Она сколько раз уложилась?
Ученики. Два раза!
Как видно из протокола, у некоторых детей в процессе обучения происходила своеобразная “сшибка” ориентиров двух типов. С одной стороны, они получили представление о необходимости специального выделения основания счета и ориентировки при счете не на отдельные предметы, а на это основание. С другой стороны, обнаруживалась ориентация на отдельность как на объект счета. Она имела место, по-видимому, в прежнем опыте ребенка. Однако, как правило, ориентация на отдельность не была устойчивой. Чаще всего ребенок поправлял сам себя: “Ой, не так! Наша мерка такая!” И, показав мерку, ребенок производил счет, приняв ее за основание. Однако отдельные рецидивы такой ошибки имели место и в последующей работе по формированию счета. Это говорит о некоторой трудности ориентации на любое заданное основание, на устойчивость прежнего способа сосчитывания “отдельностей”.
Особое место в последующей работе занимала “отделка” смысла понятия “один”. Вводились упражнения, в которых внимание детей специально обращалось на то, что измеряемый предмет можно предварительно разбить на части, каждая из которых должна быть равна мерке, а затем посчитать эти части. Каждая часть есть “один”, хотя сама может состоять из более дробных элементов. Детям показывалось, что при изменении мерки содержание “одного” также меняется, поэтому общее число частей будет другим. Дети тренировались в выделении “одного” при любой заданной мерке.
Приведем выдержку из протокольной записи урока от 3/11 1963 года. Перед каждым ребенком, как обычно, лежат наборы палочек, кубиков, кружек разного объема.
Учитель. Положите десять кубиков плотно друг к другу. Эта цепочка кубиков – наш измеряемый предмет. Покажите такую мерку (поднимает два кубика). Сколько таких мерок уложится в этой цепочке?
Саша Б. Пять!
Учитель. У тебя, Наташа?
Наташа К. Тоже пять!
Учитель. Что такое пять?
Лариса Т. Это у нас пять мерок таких уместилось на цепочке кубиков!
Учитель. Покажите один по нашей мерке! Некоторые ученики “затормозились”; одна ученица сразу подняла два кубика; Витя поднимает один кубик; через 4 сек. большинство ребят поднимает два кубика.
Учитель. Покажи, Сережа, один по нашей мерке – работай внимательно и не спеша.
Сережа П. показывает два кубика.
Учитель. А отдельный кубик можно показать?
Ученики. Нет!
Учитель. Почему?
Андрей. Нет, потому что он не равен нашей мерке.
Учитель. Галя, почему надо показать столько кубиков?
Галя. Потому что надо показать один – кусочек, как наша мерка.
Учитель. Сколько таких мерок уместилось в нашем измеряемом предмете?
Лариса. Пять!
Учитель. Витя, что надо было показать?
Витя. Один кубик.
Учитель. Оля, правильно он сказал?
Оля. Нет, нужно показать по такой мерке (показывает два кубика: Витя также поднимает два кубика).
Учитель. Теперь наша цепочка такая (пять кубиков). Это измеряемый предмет. А мерка вот какая (один кубик). Сколько раз эта мерка уложится в цепочке?
Надя. Пять мерок уложится на цепочке!
Учитель. Почему же получилось так? Тогда такая мерка была и уложилась в цепочке пять раз, а теперь такая мерка и тоже уложилась пять раз?
Слава. Тогда цепочка была большая и мерка большая, а сейчас цепочка маленькая и мерка маленькая!
Учитель. Теперь покажите из нашей цепочки “один” по такой мерке (один кубик).
Вова показывает два кубика.
Учитель. Вова, покажи всем, что ты сделал. Верно он показал, дети?
Вова хочет убрать один кубик, учитель не разрешает сделать это.
Учитель. Нет!
Учитель. Почему неверно?
Боря. Эти кубики не равны нашей мерке (Вова убирает один кубик).
Учитель. А почему же вы “один” в первый раз мне показывали так (два кубика), а во второй раз я опять прошу показать “один”, а вы мне показываете столько (один кубик)?
Наташа. Сначала мы взяли цепочку, и меркой были кубики. Значит, “один”... “один” – вот столько (показывает два кубика).
Учитель. А потом?
Юра. Мы взяли такую мерку (один кубик) Вот “один”!
Учитель. Видите, ребята, если я не знаю, какая мерка, то и не могу сказать, чему равен один.
На этом же уроке аналогичная работа проводится с меркой из четырех кубиков, сложенных квадратом. Ребята выкладывают “один” по этой мерке, затем еще “один” по этой же мерке. На вопрос: “Сколько всего?” – они отвечают: “Два”, хотя зрительно воспринимают восемь отдельных кубиков.
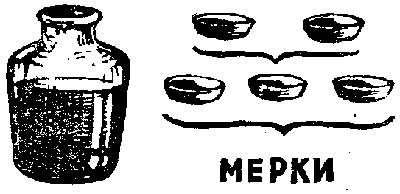
В качестве измеряемого объекта часто использовалась вода. Мерки брались составными из двух и трех чашек (рис. 4). Дети безошибочно выделяли “один” в том случае, когда выливали две чашечки, и в том случае, когда работали всеми тремя чашечками другой мерки.
Далее давалось такое контрольное задание: в качестве объекта служило написанное на доске слово “Маша”. Вначале основанием счета выступало слово, затем слог и, наконец, буква. Все ребята верно указали, что здесь “один” по первому основанию, “два” – по второму и “четыре” – по третьему 4.
На следующем уроке дети, имея один и тот же объект, работали разными мерками, “простыми” и “составными”. Они учились “объединять” и “разъединять” элементы объекта при работе с такими мерками, которые не совпадали с этими элементами.
Например,
по требованию учителя дети выкладывали на парте два квадрата из четырех
кубиков каждый.
Учитель. Это измеряемый предмет. Мерка – полоска из кубиков (рисует на
доске “пару” кубиков; рис. 5,а). Сколько раз здесь уложится наша мерка?
Ученики. Четыре!
Учитель. Измеряемый предмет тот же, а мерка другая (кубик).
Ученики. Восемь!
Учитель. Почему же получились разные числа?
Витя. Потому что мерки были разные!
Учитель. Добавьте к своим измеряемым предметам еще кубики, как на рисунке (рис. 5,б). Мерка такая. Сколько таких мерок содержится во всех ваших кубиках?
Ученики. Один..., два..., три, и еще – остаток. (Саша показывает, как получился остаток).
Учитель. Почему же эти кубики не считаете, а называете остатком?
Витя. Потому, что осталось меньше мерки, это не равно мерке!
Учитель. Теперь вы уже умеете считать разными мерками разные предметы. Чтобы не ошибиться при счете, о чем надо помнить, что знать?
Сережа. Мерку!
На специальных уроках были даны упражнения, в которых мерка либо показывалась рисунком (который тут же стирался), либо обозначалась словесно. Дети производили сосчитывание, опираясь на представляемую мерку.
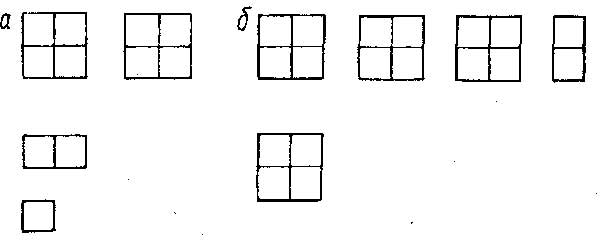
Рис. 5. Изменение числовой характеристики объекта при изменении основания счёта.
Так как ее содержание от задания к заданию менялось, то от каждого ребенка требовалась большая внимательность в определении той части предмета, которая могла быть обозначена как “один”. Почти все учащиеся безошибочно справлялись с этими заданиями. Особое внимание было уделено счету, производимому на каком-либо “натуральном” предмете при смене мерок. Так, в отношении класса нужно было произвести счет по заданиям: “Сколько всего учеников?”, “Сколько мальчиков? девочек?”, “Сколько мест (не все парты были заняты)?”, “Сколько парт?”, “Сколько рядов?” и т.д. При этом дети обосновывали тот факт, что во всех этих случаях получались разные числа.
Таким образом, в течение 9 уроков все учащиеся научились считать, опираясь на любое указанное или из практической ситуации вытекающее основание (как правило, счет далеко выходил за пределы 10). Учащиеся познакомились с формой числа, свободно переходили от одного основания счета к другому, понимая зависимость результата счета от соотношения его предмета и основания.
Задача следующей темы (10 уроков) состояла в том, чтобы показать ребенку возможность работы внутри самого числового ряда, общий принцип его образования, некоторые закономерности движения по числовому ряду. Для этого нужно “оторвать” имеющуюся у ребенка последовательность числительных от прямых задач сосчитывания конкретных объектов, т. е. придать этой последовательности собственную логику. Мы полагали, что целесообразнее всего это можно сделать путем обозначения числовой последовательности на отрезке прямой. Эта работа включала следующие этапы: 1) обучение детей умению откладывать числа на отрезке; 2) обучение умению образовывать “последующее” и “предыдущее” число по отношению к любому данному (по принципу п ± 1); 3) обучение способу сложения и вычитания чисел.
На первом этапе в процессе счета тех или иных разных предметов дети получали числа. Учитель обращал внимание на то, что, какие бы предметы ни пересчитывались и какие бы мерки ни брались, числа получаются “одинаковые” (здесь 5 – и там 5; здесь 15 – и там 15). И во всех случаях, чтобы “добраться”, например, до 5, нужно пройти от 1 до 2, от 2 до 3, от 3 до 4 и, наконец, от 4 до 5.
Учитель объяснял детям, что теперь они “посмотрят”, где могут “жить” эти числа и как они сами устроены, как можно “добираться” от одного числа до другого. После этого он показывал, что сами числа можно расположить на прямой линии, или луче (этот термин дети понимали хорошо). Но для этого нужно знать некоторые правила. Поэтому весь класс совместно с учителем “выводил” эти правила, опираясь на ранее полученные знания о способе образования самих чисел.
Понятие “один” у детей еще ранее было сформировано как обозначение части объекта, уравненной с меркой и, таким образом, не стабильной по своему содержанию. Поэтому дети поняли, что “один”, т. е. первый шаг на отрезке, может быть выбран произвольно. Когда учитель предложил затем вопрос: “Где на отрезке найти место для числа “два”?” – и отметил на линии несколько точек, явно несоответствующих “двум”, то многие дети (Сережа К., Миша П., Саша С., Юра С., Коля Ч. и др.) догадались, что при определении места для числа “два” нельзя откладывать любой отрезок. Сережа К. выразил эту мысль так: “Надо такой же кусочек взять, как и “один”!” Далее поиск места для чисел 3, 4 и т.д. все дети производили правильно. Так, на вопрос: “Сколько нужно отложить от точки числа четыре, чтобы можно было получить точку для числа пять?” – Боря К. ответил: “Сколько от нуля до одного или как от одного до двух...”
После того как детям были даны правила обозначения чисел точками на отрезке, им была показана неограниченность движения “вправо” (можно отложить любое число: и 26, и 100, и миллион).
Затем дети перешли к выполнению упражнений, в которых показывалось, что при измерении какого-либо предмета одной меркой получается и одно число (например, число три).

Рис. 6. Изображение одного и того же числа на линиях при разных “шагах”.
Но на отрезке это число можно показать по-разному – в зависимости от того, какой “шаг” мы выбрали для числа “один”. Дети, выбирая разные “шаги”, находили на разных отрезках место для одного и того же числа (рис. 6) Без особых затруднений они объясняли “причину” разного положения “трех” на каждом из отрезков (ссылка на различные “шаги”).
На последних уроках дети, изображая числа на отрезках, установили то обстоятельство, что, чем меньше число, тем оно ближе к нулю, а чем больше, тем дальше отстоит от нуля.
Приведем выдержку из протокольной записи от 8/11 1963 года.
Учитель. У меня банка с водой. Мерка – эти две маленькие баночки вместе Я буду мерить, а вы считайте про себя. Это число отложите на линии.
Ученики. Получилось пять (откладывает это число на от резке).
Учитель. С какого числа мы начинаем откладывать числа?
Леня П. С числа нуль!
Учитель. С какой стороны стою нуль?
Таня 3. С левой!
Учитель. Каким может быть первый шаг – от нуля до одного?
Вова М. Какой хотим...
Учитель. А остальные шаги тоже можем делать любыми?
Боря К. Нет, сколько отложили в первый раз, столько надо и для других чисел делать.
Учитель. А если бы мы получили не пять, а семь, где бы мы отложили число семь: ближе к нулю или дальше от нуля, чем пять?
Леня П. Дальше от нуля, чем пять.
Учитель. Почему?
Леня П. Потому что семь больше пяти...
Второй этап работы по этой теме состоял в введении формулы образования последующего и предыдущего чисел по отношению к данному. Эта работа начиналась с ознакомления детей с терминами предыдущее и последующее; предыдущее – стоящее прямо перед другим, впереди идущее; последующее – стоящее прямо после другого, сразу за другим. По указанию учителя дети называли два любых рядом стоящих числа, откладывали их на линии и определяли, какое из них предыдущее и какое последующее. Затем устанавливалось, что предыдущее число стоит ближе к нулю, а последующее – дальше от нуля.
После этого учитель давал задания: определить в отношении нескольких чисел, на сколько последующее число больше каждого данного. Сравнение каждого последующего числа с данным привело ребят к выводу, что последующее больше данного числа на единицу, и, чтобы получить последующее, необходимо к данному числу прибавить единицу.
До сих пор дети работали с отдельными конкретными числами. Необходимо было познакомить их и с буквенным изображением чисел (с самой буквенной символикой они были знакомы еще с первого полугодия, когда записывали соотношения величин). Для этого проводилась особая работа, схематически выглядевшая следующим образом.
Учащиеся по указанию учителя откладывали на числовом луче, например, число 3 при “шаге”, равном четырем клеткам тетради (точка, соответствующая этому числу, отмечалась на линии красным карандашом). Тогда дети получали новое задание: “Узнать, какое число будет стоять в этой же точке, если изменить шаг, сделать его равным двум клеткам”. С помощью учителя, выполняющего это же задание на доске, все учащиеся находили, что в “красной точке” будет стоять число 6. При этом дети свободно находили причину изменения числа – факт изменения “шага”.
В новом задании “шаг” был уже другим – шесть клеток. Красная точка теперь соответствовала и другому числу – дети вместе с учителем находили его. Это было число 2. Снова изменялся “шаг” – теперь он равен одной клетке. Большинство детей уже самостоятельно находили число 12 и ставили его у красной точки.
Учитель обращал внимание детей на то, что разными числами описывается одна и та же “красная” точка: это число может замениться другим при изменении “шага”. Учащиеся выполняли упражнения, в которых требовалось найти такой “шаг”, чтобы данная точка описывалась другим числом (в приведенном случае, например, числом 4).
Дети работали с разными лучами, те или иные точки которых специально выделялись цветными карандашами, и эти точки, меняя “шаг”, нужно было описывать разными числами (так, точка могла соответствовать числам 10, 2, 5, 1).
На основе этой работы учитель мог задать учащимся вопрос: “А как еще получить новое число?” Учащиеся вполне определенно указывали способ – взять новый “шаг”. Если они уже брали одну клетку за “шаг”, то выход был в том, чтобы взять половину клетки, тогда будет новое число. Учитель подводил учащихся к мысли о том, что “шаг” может быть взят еще меньше, тогда число будет еще больше. “Шаги” можно брать любые – дети без особых затруднений констатировали при этом, что и числа будут получаться разными, любыми. В частности, дети активно обсуждали с учителем вопрос о том, какой может быть “шаг”, если точка обозначает число “миллион”. Дети знали, что это очень большое число. Они самостоятельно сориентировались в “шаге”— он должен быть “малюсеньким-малюсеньким”.
В результате такой подготовительной работы каждый ученик имел в тетради несколько числовых лучей, на которых те или иные точки описывались разными числами. Опираясь на это, учитель показывал детям, как все эти числа можно заменить одной буквой: она говорит о любом числе. Если на луче берется точка и обозначается буквой, то здесь может стоять какое угодно число, какое именно – это зависит от “шага” (рис. 7). Такой переход к буквенному обозначению не вызвал у детей особых трудностей. Они стали выполнять упражнения по замене буквенного знака конкретными числами (меняя “шаг”, они находили, что точка А равна (2, 4 и т.д.). В специальных заданиях они заменяли “многие” числа, поставленные рядом с точкой, одним буквенным знаком. Буквы при этом использовались самые разные (А, В, n, m, I и т.д.).
После такой работы буквенные символы стали применяться учителем в упражнениях по определению “последующего” и “предыдущего” чисел. Так, давались задания: “Что нужно сделать с числом n, чтобы получить последующее число?” Большинство детей сразу догадывалось: “Нужно к n прибавить один”.
Рис. 7. Схема перехода к буквенному описанию чисел: b (или n) = 3, 6, 2, 12, 4, 1 и т.д.
Однако для некоторых детей способ образования последующего числа с “одного раза” был не совсем ясен. Потребовались отдельные дополнительные разъяснения и упражнения по образованию последующего числа по формуле n + 1, чтобы все дети усвоили ее смысл. После этого способ образования предыдущего числа (n – 1) дети под руководством учителя вывели быстро (рис. 8).
Далее дети, определяя различие между смежными числами, установили, что оно всегда равно 1. Чтобы получить каждое новое число, смежное с данным, дети делали на отрезке один “шаг” вправо или влево, т. е. прибавляли или отнимали 1. Например, дано было задание найти на отрезке точку для числа 4, потом найти точку для числа, которое на 1 больше, чем данное, и записать формулой его образование, определить это число. Дети говорили, что новое число получится по формуле 4 + 1 и оно равно 5. Далее находили число 6, производя такую запись: (4 + 1) + 1 = 6. Затем аналогичным образом отыскивалась точка для чисел 7, 8, 9, 10 и т.д.
Чтобы судить о том, как усваивается материал по этой теме, мы предложили детям в начале урока от 11/11 1963 года самостоятельную работу со следующими заданиями (работа выполнена в течение 25 мин.).
1. Даны: измеряемый предмет и мерка (планка). Требовалось произвести измерение по длине, выразить его результат числом и отложить это число на двух отрезках – в каждом случае при различном первом “шаге”.
Это задание всеми детьми было выполнено безошибочно (100 % решений).
2. На отрезке сначала нужно отложить число 5, а затем числа предыдущее и последующее. Определить каждое из них.
Здесь также было 100% решений.
3. Отложить на отрезке число К, затем число, уменьшенное на единицу и увеличенное на единицу.
Это задание выполнили 84% детей. Ошибки были следующими. Например, Наташа Г. отложила К и К + 1, но, сделав в нужном месте запись К – 1, соответствующей отметки на отрезке не сделала. Уже после контрольной работы на вопрос: “Где должно быть отмечено число К ?” — ученица нашла нужную точку правильно. У Оли Б. произошел своеобразный “перенос” условия предыдущего задания. Она поставила число К на том же расстоянии от начала отрезка, как в предыдущем задании число 5, и отметила точки для числа, уменьшенного на единицу (4) и увеличенного на единицу (6). Остальные дети, не справившиеся с заданием, чаще всего делали такую ошибку: выбрав произвольно точку для числа К., пытались затем находить точки для новых чисел, отправляясь от начала отрезка, как это делается для определения положения известного конкретного числа.
Таким образом, умение “находить” точку для произвольно выбранного числа некоторыми слабыми учениками усваивалось с трудом.
4. Отложить на отрезке число Р, а затем число, увеличенное на 4 и уменьшенное на 3.
Это задание выполнил 81 % детей. Характерная ошибка такова. Например, двое учащихся Р и Р + 4 отложили правильно, но Р – 3 они не откладывали вовсе. Два ученика отложили от числа Р по одинаковому отрезку направо и налево, написав: Р + 4 и Р – 3. Один ученик правильно двигался по отрезку и сделал нужное число шагов (4 шага вправо от числа Р и 3 шага влево), но запись выполнил неверно (вместо “—З” записал “—1”).
Общие результаты выполнения этих заданий показывают, что в процессе обучения большинство детей усвоило то, что результат измерения любых величин можно выразить соответствующими точками линии. Дети усвоили принцип образования чисел при движении по отрезку прямой.
Следующая тема включала усвоение зависимостей между величиной (объектом), меркой и числом (дети оценивали соотношение мерок при одной величине объекта и разных числах или соотношение величины объектов при одинаковых мерках, но разных числах и т. д.). Эта работа проводилась таким образом. Детям были даны задания, требующие проведения счета по разным основаниям (предлагались разные мерки). Когда ученики находили результат (разные числа), учитель ставил вопрос: “Почему при счете получаются разные числа – то большие, то маленькие?” Приведем выдержку из протокольной записи урока от 21/11 1963 г., на котором проводилась работа по указанной теме.
Ученики (отвечают на вопрос). Потому, что мы брали разные мерки.
Учитель. Когда число шесть получили – какая была мерка?
Наташа П. Маленькая.
Учитель. А число три?
Таня 3. Мерка здесь больше...
Учитель. Если мы получили число больше, то какая мерка была?
Надя М. Меньше!
Учитель. А если число получили маленькое, то какая была мерка?
Жора Т. Больше!
Учитель. Записывается все это по-особенному, ребята, вот так (пишет и говорит):
Ае = 6. Предмет можно обозначить любой буквой, например А, мерку также любой буквой, пишем ее здесь (показывает). Эта запись означает, что предмет А при мерке е равен шести. Повторите!
Ученики. Предмет А при мерке е равен шести.
Учитель. Что вы сейчас делали?
Андрей Д. Измеряли палочку.
Учитель. Чем мы измеряли палочку?
Боря К. Меркой е.
Учитель. Какое число получили?
Лена П. Число шесть.
Учитель. Как же мы запишем это? Прочти, Витя!
Витя М. Предмет А при мерке е равен шести.
Учитель. Потом какой предмет мы измеряли?
Саша Б. Тот же предмет А!
Учитель. Мерку обозначим буквой г. Как теперь я могу записать?
Боря К. Предмет
А, измеряемый меркой г, равен числу три.
Учитель записывает Аг = 3. Запишите!
Ae = 6
Aг = 3
Учитель. При маленькой мерке число получается какое?
Ученики. Больше!
Учитель. А при большей мерке?
Ученики. Меньше!
Подобные отношения дети устанавливали, промеривая один и тот же объем воды разными мерками или пересчитывая один и тот же ряд кубиков при разном основании счета. Найденные отношения между мерками обозначались знаками “больше” или “меньше”. Например, в случае, когда были даны мерки к и г, дети делали заключение:
Мк = 3
Мг = 4
-------------
значит, к > г
Тренировка в выявлении зависимости между измеряемым объектом, меркой и числом происходила при решении задач, требующих оценки этой зависимости. Например, на уроке, проведенном 23/11 1963 года, решались следующие задачи.
Учитель. На сборе октябрят надо было делать елочные украшения – фигурки. Учительница дала Наташе бумажную полоску. Обозначим ее длину какой-нибудь буквой. Какой?
Ученики. Буквой А!
Учитель. Надо было сделать четыре фигурки. На сколько частей нужно разрезать полоску?
Наташа Г. На четыре части.
Учитель. У Наташи есть мерка б и если ею померить полоску, то получается как раз четыре куска. Как это можно записать формулой?
Коля Ч. Предмет А при мерке б равен четырем.
Учитель. Но делать фигурки пришли пятеро октябрят. Может Наташа по этой мерке дать бумажные кусочки всем пяти ребятам?
Надя М. Нет!
Учитель. Что же она должна сделать?
Леня В. Взять другую мерку!
Учитель. Какую?
Миша П. Меньшую.
Учитель. Почему?
Коля Н. Потому что кусочков надо больше.
Учитель. Как это записать?
Юра С. А при к равно пяти.
Учитель. Один и тот же измеряемый предмет – Наташина полоска, а числа получаются разные. Почему это?
Вова М. Потому что мерки разные.
Учитель. Что можно сказать про мерки?
Ученики. Мерка б больше, мерка к меньше.
Учитель. Если измеряемый предмет один и тот же, то что можно сказать про числа, получаемые при этих мерках?
Юра С. Число получается больше, если мерка меньше, потому что маленькую мерку можно больше раз уместить на полоске.
Учитель. Сравните мерки б и к.
Ученики записывают: б > к.
В последующих заданиях зависимость между мерками и числами нужно было находить без опоры на предварительную работу с предметами – условия давались только формулами. Большинство учащихся правильно и быстро оценивало имеющуюся зависимость.
Оценка зависимости изменения числа от изменения предмета при сохранении мерки вначале происходила на основе работы с предметным материалом. При помощи учителя дети сформулировали правило: если меняется предмет, а мерка остается той же, то меняется и число. При увеличении предмета и число становится больше. Если же предмет уменьшается, то и число становится меньше 5.
Следует отметить, что при работе с предметными пособиями дети легко справлялись с оценкой разных видов отношений. Однако при необходимости установить отношение, условие которого задавалось лишь формулами, некоторые слабые учащиеся (например, Витя М., Надя М., Алла К., Наташа Г. и др. – всего 5-6 детей) делали ошибки. Чаще всего эти дети ориентировались лишь на связь двух компонентов – числа и мерки (если число больше, то мерка меньше) и не умели оценивать правильно зависимости трех компонентов.
Понадобилась дополнительная работа с этими детьми, чтобы они уяснили необходимость учитывать зависимость трех компонентов: предмета, мерки и числа.
При работе по этой теме было проведено четыре тренировочных урока, на которых дети решали задачи, содержащие разнообразные зависимости указанных компонентов. Например, учитель предлагал задачу: “Предмет Б, измеряемый меркой е, равен трем. Взяли другую мерку – г, которая меньше е. Какое число могло получиться при новой мерке — может быть, шесть? Может быть, один? Что правильно? Запишите”. Дети записывают формулы, делают вывод 6.
Бе = 3
г > е
Бг = 6
Учитель. Почему поставили число шесть, а не число один?
Наташа П. Мерка г меньше, а измеряемый предмет какой и был. Маленькая мерочка помещается на предмете больше раз.
Учитель. Если бы здесь было число один (вместо 6 вставляет 1), то тогда какая бы была мерка г?
Юра С. Тогда мерка г была бы больше мерки е.
На следующих уроках вводились задания (вначале опять на предметном материале), в которых необходимо было оценить соотношение величины предметов, когда числа одинаковые, а мерки разные, хотя известно их соотношение (одна мерка больше-меньше другой). Затем подобные задания выполнялись при наличии одних формул, фиксирующих условия.
В конце всей работы по этой теме дети умели решать примеры следующих типов:
1) Даны одинаковые предметы, разные мерки и разные числа. Установить отношение мерок.
Ак = 7
Аг = 12
-------
к ... г
Задача может быть обратной: дано отношение мерок при одинаковых предметах; установить отношение чисел.
Ак = 7
Аг = ...
-------
к < г
2) Даны разные предметы и разные числа. Мерки одинаковые. Установить отношение предметов.
Мк = 7
Дк = 9
-------
М ... Д
Задача может быть обратной: даны разные предметы и одинаковые мерки, дано отношение предметов, установить отношение чисел.
Мк = 7
Дк = ...
-------
М < Д
3) Даны одинаковые числа, разные предметы и мерки. Дано отношение мерок. Установить отношение предметов.
Бе = 8
Мг = 8
е > г
-------
Б ... М
Задача может быть обратной: даны одинаковые числа, разные предметы и мерки, дано отношение предметов; установить отношение мерок.
Бе = 8
Мг = 8
М > Б
-------
е ... г
Работа по закреплению правил, фиксирующих определенные зависимости между предметом, меркой и числом, проходила в процессе разнообразных упражнений, выявляющих различные виды таких зависимостей. Особое внимание было уделено формированию у детей умения четко анализировать содержание формул, умения выделять их постоянные и переменные элементы. Приведем выдержку из протокольной записи одного из последних уроков по этой теме (от 1/11 1963 года).
Учитель.
Восемнадцать девочек первых классов готовят к празднику танец с ленточками.
Девочки принесли ленты. Лена принесла красную ленту – вот такую, рисует
на доске). Обозначим ее длину А. Лена взяла мерку к, по
ней разрезала ленту на восемнадцать кусочков и раздала эти кусочки подругам.
Запишите все это формулой.
Ученики записывают: Ак = 18.
Учитель. Потом Лена взяла синюю ленту – такую (рисует на доске). Обозначим ее длину буквой Б – эта лента короче. Ее также нужно разделить поровну между всеми девочками. Можно ли это сделать той же меркой к?
Наташа Г. Нет! Надо взять мерку поменьше.
Учитель. Верно. Другую мерку обозначим е. Что можно записать про мерки?
Таня 3. Мерка е меньше мерки к.
Учитель. Запишите формулой, как вы получили число.
Ученики записывают самостоятельно: Бе = 18. Учитель. Что одинакового в этих формулах? Леня В. Числа!
Учитель. Что изменилось?
Надя К. Длина ленты!
Учитель. Как это записать?
Ученики. Предмет А больше предмета Б.
Учитель. Числа же одинаковые!
Ученики. Но мерки разные – е меньше к.
Учитель. Сейчас я запишу формулы, а вы вставьте нужные знаки. Только смотрите внимательно на то, что остается тем же самым – предмет, мерка или число.
Ак = 7
Аг = 12
-------
к ... г
Что здесь одинаковое?
Ученики. Измеряемые предметы!
Учитель. А что разное?
Ученики. Числа и мерки.
Учитель. Если при одинаковых предметах получились разные числа, то что можно сказать про мерки?
Ученики. Они разные!
Учитель. Сравните мерки – поставьте нужный знак. Ученики записывают: к > г.
Учитель. Новое задание: Что здесь одинаковое?
Мк = 6
Дк = 9
-------
М ... Д
Лена М. Мерки!
Учитель. А что изменилось?
Наташа П. Предметы и числа.
Учитель. Если мерки одинаковые, то большее число получится от какого предмета?
Витя М. Если число больше, то и предмет больше.
Учитель. Какой же знак нужно поставить? Ученики записывают: М < Д.
Подобные упражнения проводились как при наличии только одних формул, так и при демонстрации необходимых зависимостей на предметном материале. Последнее проводилось в тех случаях, когда словесная формулировка той или иной зависимости представляла для некоторых детей известные трудности. К концу работы по этой теме некоторые дети (3—4 учащихся из класса) с трудом давали развернутую словесную формулировку зависимости между предметом, меркой и числом. На вопросы учителя эти дети в большинстве случаев отвечали правильно. Таким образом, формирование развернутого рассуждения, связанного с изучаемыми зависимостями между объектом, мерой и числом, требовало от учителя особого внимания и применения специальных приемов, облегчающих детям “улавливание” этих зависимостей, наталкивающих на правильные выводы из указанных условий, помогающих анализировать изменения в формулах.
Весь раздел программы, связанный с введением чисел, был пройден за 32 урока (к 5/11 1963 года).
Вслед за этим шел раздел “Сложение и вычитание чисел” (описание усвоения этого раздела не является предметом данной книги).
Через месяц после окончания работы по рассмотренному разделу всем 32 учащимся нашего класса была предложена контрольная работа, состоящая из следующих заданий 1-5 (в скобках показано решение):
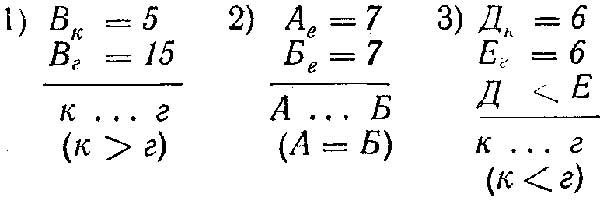
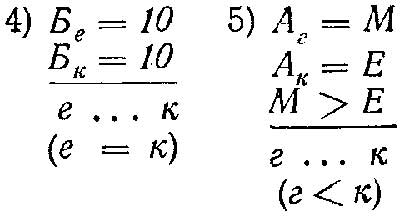
6) Отложить на отрезке число 3 при “шаге”, равном двум клеточкам (тетради). На другом отрезке это же число отложить при “шаге” в четыре клеточки.
После того как учащиеся выполнили это задание, учитель продолжил: “Даю также формулы:
Ак = 3
... к = 3
В первой формуле показано, что число три – оно отмечено на первой линии – получено при измерении какого-то предмета А меркой к. Во второй формуле показано, что число три, изображенное на второй линии, получено при измерении предмета той же меркой к. Обозначьте, каким здесь был измеряемый предмет” (измеряемый предмет был тем же самым).
В эту контрольную были включены задания, ранее не встречавшиеся учащимся (задания 4 и 5). Форма заданий также была необычна. Так, задания 4 и 6 содержали моменты “сбивающего” характера. В задании 4, например, дан один и тот же предмет Б и даны одинаковые числа при мерках, обозначенных разными буквами, что обычно свидетельствует и о разной величине мерок. Однако из анализа имеющихся соотношений следует равенство мерок – именно это дети и должны установить (такого задания в ходе обучения дети не выполняли). В задании 6 на двух отрезках дети откладывают одно и то же число 3, но выполняют это при разном масштабе. Когда учитель дает формулы, изображающие “получение” этого числа, и требует определения “второго” предмета, дети могут “сбиться” на то, что второй измеряемый предмет больше первого.
Предлагая эту работу повышенной трудности, мы стремились установить действительный характер усвоения материала того раздела, который связан со счетом и числом.
В табл. 1 приводятся данные о количестве учащихся, справившихся и не справившихся с заданиями.
|
Задания
|
Количество
учащихся
|
||
|
выполнивших
задание правильно |
самостоятельно
исправивших ошибку
|
выполнивших
задание неправильно |
|
|
1
|
29
|
2
|
1
|
|
2
|
31
|
--
|
1
|
|
3
|
28
|
--
|
4
|
|
4
|
21
|
3
|
8
|
|
5
|
14
|
6
|
12
|
|
6
|
25
|
--
|
7
|
Из общего числа (192) возможных ошибок (6 решений у каждого из 32 учеников) фактически было допущено 33 ошибки, т.е. 17%. Таким образом, правильных решений было 83 %. Наибольшее число ошибок, как и следовало ожидать, было сделано в новом, 5-м задании и в заданиях 4 и 6, являющихся особенно трудными. В таблице 2 приведены данные о распределении ошибок (самостоятельное исправление мы принимаем здесь за правильное решение).
|
Количество
учащихся, выполнивших работу
|
|||
|
без
ошибок
|
с
1 ошибкой
|
с
2 ошибками
|
с
3 ошибками
|
|
15
|
5
|
8
|
4
|
Как показывают эти данные, 15 человек всю работу выполнили правильно (правда, 9 из них имели по одному исправлению). Причем больше всего ошибок (12 из 33) сделали 4 ученика, которые, очевидно, усвоили тему недостаточно хорошо (их работы оценены “тройками”). Это были те учащиеся, которые к концу изучения темы не формулировали словесно правил о соотношении величины, мерки и числа.
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
Статья
рекомендована для публикации Б.Д. Элькониным и Л.В. Берцфаи.
Статья
взята из книги «Возрастные возможности усвоения знаний (младшие классы
школы)».
Под редакцией Д.Б. Эльконина и В.В. Давыдова, «Просвящение» – Москва,
1966.
ЛИТЕРАТУРА
1. Гальперин
П.Я. и Георгиев Л.С., К вопросу о формировании начальных математических
понятий // Сообщения и доклады АПН РСФСР – 1960 – № 1, 3, 4, 5, 6.
2. Давыдов В.В. Анализ строения счета как предпосылка построения программы
по арифметике. // Вопросы психологии учебной деятельности младших школьников.
– М.: АПН РСФСР, 1962.
3. Давыдов В.В. О психологическом анализе содержания действий // Тезисы
докладов на II съезде Общества психологов. Вып. 2 – М.: АПН РСФСР, 1963.
4. Давыдов В.В. Опыт введения элементов алгебры в начальной школе. Советская
педагогика – 1962 – № 8.
5. Орлова Е.С. Обучение счету на основе измерения. // Наш опыт учебно-воспитательной
работы в школе. – М.: АПН РСФСР, 1962.
6. Пчелко А.С. и Поляк Г.Б. Арифметика. Учебник для I класса начальной
школы. – М.: Учпедгиз, 1963.
7. Пчелко А.С. Методика преподавания арифметики в начальной школе. – М.:
Учпедгиз, 1953.
8. Фролова Т. А. Опыт введения буквенной символики при обучении математике
в I классе. // Повышение эффективности обучения в начальной школе. – М.:
АПН РСФСР, 1963.
1.
Наиболее последовательно эта теория абстракции была в свое время проведена
немецкими методистами (Грубе, Лай). Так называемые "числовые фигуры",
имеющиеся в наших учебниках, являются отзвуком этой теории и соответствующей
ей системы дидактических пособий.
2. В предыдущие годы сходная по замыслу экспериментальная
работа была проведена в детских садах П.Я. Гальпериным и Л.С. Георгиевым
[1].
3. Теоретическое обоснование целесообразности и правомерностим
подобного построения курса, а также некоторые результаты работы по экспериментальной
программе изложены в статьях В.В. Давыдова [4] и Т.А. Фроловой [8].
4. Сами дети эти основания обозначалаи словом "мерка".
Мы понимаем некоторую терминологическую неадекватность, имеющую здесь
место, но в настоящее время не можем дать другого, более точного термина.
5. При этом, конечно, специально показывалось детям то
обстоятельство, что изменение числа (целого) возможно только при изменении
предмета на величину, равную или превышающую заданную мерку (основание
счета).
6. К этому времени учащиеся знали, что при изменении мерки
число может изменяться на разное количество единиц - важно лишь установить
направление этого изменения (больше или меньше данного числа будет новое
число). Конкретное соотношение между мерками и числами (например, их взаимное
изменение в 2 или 3 раза) еще не изучалось.